Inverse of a Function & Restricted Domain

Inverse of a Function

When x is interchanged with y in the equation of a function y = f(x), it's reflected in the mirror line y = x. This is called an inverse function.

Find the inverse equation of f(x) = x² - 2

First, change the f(x) to y, since y = f(x).

f(x) = x² - 2
y = x² - 2

Second, switch the x variable with the y variable.

y = x² - 2
x = y² - 2

Third, isolate the y variable.

x = y² - 2
x + 2 = y²

±√ x + 2 = √y²
±√ x + 2 = y

y = ±√ x + 2

The inverse of f(x) = x² - 2 would be y = ±√ x + 2

Be careful, not all inverses are functions. If we were to perform a horizontal line test and it 'hits' two points on the graph, the inverse of the graph will not be a function.

If we were to graph our original equation, f(x) = x² - 2 its inverse would not be a function because two points hit the horizontal line test. Or if we were to graph the inverse y = f(x)-¹, it would also fail the vertical line test because there must only be one y-value for every x-value.

Tip: The inverse of multiply is divide and the inverse of addition is subtraction.

e.g., f(x) = 2x + 3

The inverse of  f(x) would be f(x)-¹ = ¹⁄₂ x - ³⁄₂

If you were given a question on how you would get the inverse to be a function then this is where restriction comes in.

Also another way to determine the domain and range of the inverse of f(x) is to switch the domain and range of f(x).
e.g., 
f(x)
D: {x | x∈R} or (-∞, ∞)
R: {y | y ≥ 0, y∈R} or [0, ∞)

f(x)-¹
D: {x | x ≥ 0, x∈R} or [0, ∞)
R: {y | y∈R} or (-∞, ∞)

Restricted Domain

Domain is the set of all possible values for the independent variable in a relation. This would be the x-values.

So now that we know that our inverse isn't a function, how would we restrict the domain so that the inverse of f(x) is a function?

Well, we could achieve this by using one side of the parabola, we could use the left side of the parabola (-∞,0] or we could use the right side of the parabola [0,∞).

If we were to use the right side of the parabola, then we would restrict our domain to [0, ∞) or { x | x ≥ 0, x∈R}.

 

We would write, "Restrict the domain of f(x) to [0, ∞)", so that the inverse will become a function.

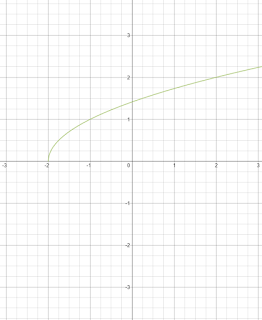
Now if we were to graph our inverse y = ±√ x + 2 , we would use the y = √ x + 2 and not y = -√ x + 2 because we restricted our graph so that the positive values are left. Our inverse would now look like this. We could also just switch the x and y values of the restricted function and we would still get the same answer.

Now, the inverse is a function! Yay!

Now let's start from the beginning.

1. Find the inverse equation of f(x) = x² - 2

f(x) = x² - 2

y = x² - 2

x = y² - 2

x + 2 = y² 

±√ x + 2 = √y²
±√ x + 2 = y
y = ±√ x + 2

2. Restrict the domain of f(x) so that the inverse will become a function.

Restrict the domain of f(x) to [0, ∞)
y = + √ x + 2

3. List the domain and range of f(x) and its inverse.
f(x)
D: {x | x∈R} or (-∞, ∞)
R: {y | y ≥ -2, y∈R} or [-2, ∞)

f(x)-¹
D: {x | x ≥ -2, x∈R} or [-2, ∞)
R: {y | y∈R} or (-∞, ∞)

4. List the domain and range of the restricted domain of f(x) and its inverse.
f(x)
D: {x | x ≥ 0, x∈R} or [0, ∞)
R: {y | y ≥ -2, y∈R} or [-2, ∞)

f(x)-¹
D: {x | x ≥ -2, x∈R} or [-2, ∞)
R: {y | y ≥ 0, y∈R} or [0, ∞)